Isaac Newton Biography | facts and Gravity Laws Our National Heroes

Introduction:

Isaac Newton was a Physicist and Mathematician, developed many scientific works related to human life. He was a mathematician, Physicist, and more he was famous for the laws of motion. Credited as one of the greatest minds of the 17th century in the Scientific Revolution. Let’s talk about his famous inventions like laws of motion, gravity, and other such types of inventions. Here, we discuss Isaac Newton Biography | facts and Gravity Laws.

Basic Information	Isaac Newton
Nationality	British, England
Date of Birth	4th January 1643
Place of Birth	Wools Thorpe-by-Colsterworth, Lincolnshire, England
Date of Death	31st March 1727
Place of Death	Kensington, Middlesex, Great Britain
Cause of Death	Natural
Age	84 years old
School	The King’s School, Grantham
High School / College	Trinity College, Cambridge (M.A., 1668)
University	Royal Society,Royal Mint
Occupation	Scientist, Inventor
Career	1669 – 1727
Famous for	Newtonian mechanics, Newton’s laws of motion
Title	Gravity Inventor
Other works	Physics,Natural philosophy,Alchemy,Theology,Mathematics,Astronomy,Economics
Spouse	He did not marry
Awards	FRS (1672),Knight Bachelor (1705)

Early life and family:

Newton was born on 4th January 1643, in Woolsthorpe, Lincolnshire, England. Using the “old” Julian schedule, Newton’s introduction to the world date sometimes shown as 25th December 1642. Newton was the main child of a prosperous neighborhood rancher, likewise named Isaac. Who passed on a quarter of a year before he was born. An untimely infant brought into the world little and frail, Newton not expected to endure^[1].

Isaac Newton, real image of ancient times

At the point when he was 3 years of age, his mom, Hannah Ayscough Newton. Remarried a wealthy pastor, Barnabas Smith, and went to live with him, leaving youthful Newton with his maternal grandmother. The experience left a permanent engraving on Newton, later showing itself as an intense feeling of frailty. He restlessly fixated on his distributed work, shielding its benefits with unreasonable conduct^[1].

At age 12, Newton brought together with his mom after her second husband died. She brought along her three little youngsters from her subsequent marriage^[1].

Isaac Newton’s Education:

Newton selected at the King’s School in Grantham, a town in Lincolnshire. Where he held up with a neighborhood pharmacist and acquainted with the entrancing universe of science.

His mother pulled him out of school at age 12. She made him a rancher and have him tend the homestead. Newton bombed pitiably, as he discovered cultivating dull. Newton was before long sent back to King’s School to complete his essential training.

Maybe detecting the youngster’s natural scholarly capacities. His uncle, an alum of the University of Cambridge’s Trinity College, born Newton’s mom to have him enter the college. Newton selected a program like a work-concentrate in 1661. Therefore, looked out for tables and dealt with wealthier understudies’ rooms^[1].

Scientific Revolution:

At the point when Newton showed up at Cambridge, the Scientific Revolution of the seventeenth century was at that point in full power. The heliocentric perspective on the universe conjectured by cosmologists Nicolaus Copernicus and Johannes Kepler and later refined by Galileo, was notable in most European scholarly circles^[1].

Isaac Newton sunlight study optics prism engraving 1879

Scholar René Descartes had planned another idea of nature as a multifaceted, indifferent, and inactive machine. However, like most colleges in Europe, Cambridge saturated with the Aristotelian way of thinking and a perspective on nature laying on a geocentric perspective on the universe, managing nature is subjective instead of quantitative terms^[1].

During his initial three years at Cambridge, Newton shown the standard educational plan yet was interested in the further developed science. All his extra time spent perusing from the advanced logicians. The outcome was not exactly heavenly execution, yet justifiable one, given his double course of study^[1].

Arrangement of Notes and Questionnaires:

It was during this time that Newton kept a second arrangement of notes, named “Quaestiones Quaedam Philosophical” (“Certain Philosophical Questions”). The “Quaestiones” uncover that Newton had found the new idea of nature that gave the system to the Scientific Revolution. Even though Newton graduated without praises or differentiations, his endeavors won him the title of researcher and four years of monetary help for future instruction.

In 1665, the bubonic plague that was desolating Europe had come to Cambridge, constraining the college to close. Following a two-year break, Newton got back to Cambridge in 1667 and chosen a minor individual at Trinity College, as he as yet not considered a champion researcher^[1].

Master of Arts Degree:

In the resulting years, his fortune improved. Newton got his Master of Arts degree in 1669, preceding he was 27. During this time, he went over Nicholas Mercator’s distributed book on techniques for managing boundless arrangement^[2].

Famous scientist Mathematician, Physicist and Scientist, Isaac Newton

Newton immediately composed a composition, De Analysi, explaining his own more extensive running outcomes. He imparted this to companion and coach Isaac Barrow, however, excluded his name as creator^[2].

In June 1669, Barrow imparted the unaccredited composition to British mathematician John Collins. In August 1669, Barrow recognized its creator to Collins as “Mr. Newton … young … of an exceptional virtuoso and capability in these things. “

Newton’s work brought to the consideration of the arithmetic network unexpectedly. Without further ado subsequently, Barrow surrendered his Lucasian residency at Cambridge, and Newton expected the seat^[1].

Isaac Newton’s Inventions:

Newton’s first significant public logical accomplishment was planning and developing a reflecting telescope in 1668. As a teacher at Cambridge, Newton needed to convey a yearly course of talks and picked optics as his underlying point. He used his telescope to contemplate optics and help show his hypothesis of light and shading.

The Royal Society requested an exhibition of his reflecting telescope in 1671, and the association’s advantage urged Newton to distribute his notes on light, optics, and shading in 1672. These notes later distributed as a component of Newton’s Opticks: Or, A composition of the Reflections, Refractions, Inflections, and Colors of Light^[1].

The Apple Myth:

Somewhere between 1665 and 1667, Newton got back from Trinity College to seek after his private investigation, as school shut because of the Great Plague. Legend has it that, right now, Newton encountered his acclaimed motivation of gravity with the falling apple. As per this normal fantasy, Newton was sitting under an apple tree when a natural product fell and hit him on the head, moving him to out of nowhere to concoct the hypothesis of gravity.

While there is no proof that the apple hit Newton on the head, he saw an apple tumble from a tree, driving him to ask why it fell straight down and not at a point. Therefore, he started investigating the hypotheses of movement and gravity^[1].

Publications of Material Science book:

It was during this 18-month rest as an understudy that Newton imagined a significant number of his most significant bits of knowledge including the strategy for minuscule analytics, the establishments for his hypothesis of light and shading, and the laws of planetary movement that ultimately prompted the distribution of his material science book Principia and his hypothesis of gravity^[1].

Isaac Newton’s Laws of Motion:

Newton was following for 18 months in 1867, which is effectively nonstop work. Newton Published Philosophiae Naturalis Principia Mathematica (Mathematical Principles of Natural Philosophy), most frequently recognized as Principia Mathematica.

Principia supposed to be the absolute most interesting book on physical science and perhaps the entirety of science. Its distribution promptly raised Newton to global unmistakable quality^[2].

Principia offers an accurate quantitative portrayal of bodies moving, with three fundamental yet significant laws of movement^[1]:

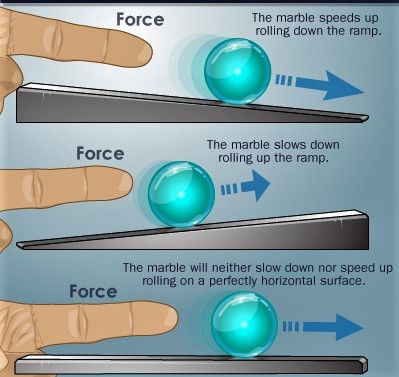
Newton’s first law:

The first law specifies that an object at other will stay at rest, and an object in motion will remain in motion unless carried out on by a net external force. Mathematically, this is equal to saying that if the net impose on an object is zero, then the velocity of the object is consistent^[2].

\sum \mathbf {F} =0\;\Leftrightarrow \;{\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}=0.

where F is the force being applied is notation for summation), is the velocity, and is the derivative of regarding time .

Newton’s first law often referred to as the principle of inertia.

Newton’s first (and second) laws are valid only in an inertial reference frame.

Newton's First Law (Law of Inertia) — Newton’s First Law (Law of Inertia)

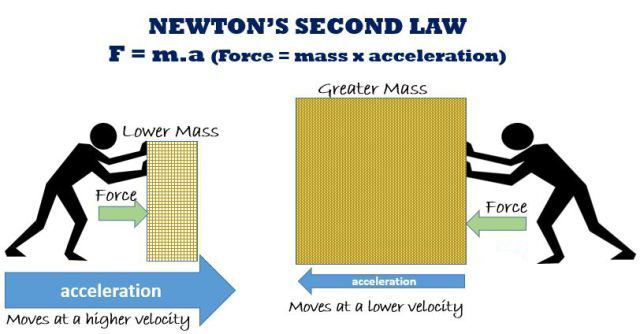
Newton’s Second Law:

Power is equivalent to mass occasions increasing speed, and a change moving (i.e., change in speed) is corresponding to the power applied^[1].

The second law states that the rate of change of energy of a body over time is shortly comparable to the force involved and develops in the same way as the employed force.

$\mathbf {F} ={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}$

where $\mathbf {p}$ is the momentum of the body,

Constant Mass

For objects and systems with constant mass, the second law can re-stated in terms of an object’s acceleration.

$\mathbf {F} ={\frac {\mathrm {d} (m\mathbf {v} )}{\mathrm {d} t}}=m\,{\frac {\,\mathrm {d} \mathbf {v} \,}{\mathrm {d} t}}=m\mathbf {a} ,$

where F is the net force employed, m is the mass of the body, and a is the body’s acceleration. Thus, the net force committed to a body makes a corresponding acceleration.

Variable-mass systems

Variable-mass systems, like a rocket burning fuel and eliminating used gases, are not closed and cannot immediately used by organizing mass a function of time in the second law; The equation of motion for a body whose mass m varies with time by either eliminating or accreting mass got by giving the second law to the entire, eternal-mass system comprising the body and its ejected or accreted mass; the result is[3]

$\mathbf {F} +\mathbf {u} {\frac {\mathrm {d} m}{\mathrm {d} t}}=m{\mathrm {d} \mathbf {v} \over \mathrm {d} t}$

where u is the drain velocity of the emerging or incoming mass relative to the body. From this equation one can determine the equation of motion for a changing mass system, for example, the Tsiolkovsky rocket equation.

Under some laws, the quantity $\mathbf {u} {\frac {\mathrm {d} m}{\mathrm {d} t}}$ on the left-hand side, which describes the advection of power, defined as a force (the force exerted on the body by the changing mass, such as rocket exhaust) and entered the quantity F. Then, by swapping the definition of acceleration, the equation becomes F = ma[3].

Newton's 2nd Law of Motion — Newton’s 2nd Law of Motion

Newton’s Third Law of Motion:

Power is a push or pull following up on an item bringing about its association with another article. The Power is an after effect of a cooperation. Power can be ordered into two classifications: contact power, for example, frictional power and non-contact power like gravitational power. As per Newton, when two bodies interface, they apply power on one another, and these powers are known as activity and response sets, which is clarified in Newton’s third law of movement^[3].

Newton’s third law of movement stated that:

“When one body exerts a force on the other body, the first body experiences a force which is equal in magnitude in the opposite direction of the force which is exerted”.

The above assertion implies that in each cooperation, there is a couple of powers following up on the connecting objects. The size of the powers are equivalent and the heading of the power on the principal object is inverse to the bearing of the power on the subsequent item[3].

For Example:

A Person drives a cart, Cart 1, to one side while pushing another cart, Cart 2, that has a huge cooler on it. They all out mass of Cart 2, truck besides cooler, is multiple times the absolute mass of Cart 1, truck besides individual. If the individual is driving with sufficient power that the two carts speed up to one side, what we can say without a doubt about the extents of the powers on the carts?[3]

Newton and the Theory of Gravity:

Newton’s three essential laws of movement illustrated in Principia helped him show up at his hypothesis of gravity. Newton’s law of general attractive energy expresses that two items draw in one another with a power of gravitational fascination that is corresponding to their masses and contrarily relative to the square of the separation between their focuses.

These laws clarified curved planetary circles, as well as practically every other movement, known to man: how the planets kept in a circle by the draw of the sun’s gravity; how the moon spins around Earth and the moons of Jupiter rotate around it; and how comets spin in circular circles around the sun[3].

They likewise permitted him to find out the mass of every planet, compute the leveling of the Earth at the shafts and the lump at the equator, and how the gravitational draw of the sun and moon make the Earth’s tides. In Newton’s record, gravity kept the universe adjusted, made it work, and united paradise and Earth in one incredible condition^[1].

Isaac Newton and Robert Hooke:

Isaac Newton who was an enlightenment hero

Not every person at the Royal Academy was energetic about Newton’s disclosures in optics and 1672 distribution of Opticks: Or, A composition of the Reflections, Refractions, Inflections and Colors of Light. Among the protesters was Robert Hooke, one of the first individuals from the Royal Academy and a researcher who cultivated in various territories, including mechanics and optics.

While Newton guessed that light made of particles, Hooke trusted it made of waves. Hooke immediately censured Newton’s paper in designing terms and assaulted Newton’s strategy and ends^[1].

Newton’s work in Optics:

Hooke was not the only one to scrutinize Newton’s work in optics. Prestigious Dutch researcher Christiaan Huygens and various French Jesuits likewise brought up criticisms. But since of Hooke’s relationship with the Royal Society and his work in optics, his analysis stung Newton the most exceedingly awful.

Incapable to deal with the evaluation, he went into a fierceness, a response to analysis that was to proceed for the duration of his life. Newton denied Hooke’s charge that his hypotheses had any weaknesses and contended the significance of his revelations to the entirety of science.

In the following months, the trade between the two men developed more caustic, and soon Newton took steps to stop the Royal Society out and out. He stayed just when a few different individuals guaranteed him that the Fellows held him in high regard^[1].

Competition between Newton and Hooke:

The competition between Newton and Hooke would proceed for quite a while from that point. At that point, in 1678, Newton endured a total mental meltdown, and the correspondence unexpectedly finished. The passing of his mom the next year made him significantly more separated, and for a very long time he pulled out from scholarly trade aside from when others started correspondence, which he kept short^[1].

During his rest from public life, Newton got back to his investigation of attraction and its consequences for the circles of planets. Unexpectedly, the impulse that put Newton on the correct course in this investigation came from Robert Hooke^[1].

Royal Society meeting:

In a 1679 letter of general correspondence to Royal Society individuals for commitments, Hooke kept in touch with Newton and raised the subject of planetary movement, proposing that an equation including the converse squares may clarify the fascination among planets and the state of their circles.

Newton works on Prism — Newton worked on Prism

Resulting trades happened before Newton immediately severed the correspondence indeed. Hooke’s thought was before long fused into Newton’s work on planetary movement, and from his notes, it shows up he had immediately made his inferences by 1680, however; he hushed up his disclosures^[1].

In mid-1684, in a discussion with individual Royal Society individuals Christopher Wren and Edmond Halley, Hooke put forth his defense on the evidence for planetary movement.

Both Wren and Halley thought he was on to something, however, called attention to that a numerical exhibit was required^[1].

Visiting Cambridge University:

In August 1684, Halley headed out to Cambridge to visit with Newton, who was emerging from his confinement. Halley inactively asked him what shape the circle of a planet would take if its appreciation for the sun followed the converse square of the separation between them (Hooke’s hypothesis).

Newton knew the response, because of his concentrated work for as long as six years, and answered, “A circle.” Newton professed to have tackled the issue nearly 18 years earlier, during his break from Cambridge and the plague, yet he couldn’t discover his notes. Halley convinced him to work out the issue numerically and offered to pay all expenses so the thoughts may distribute, which it was, in Newton’s Principia^[1].

President in the Royal Society:

Newton became the President of the Royal Society after Hooke’s death in 1703. Newton never appeared to comprehend the idea of science as an agreeable endeavor, and his aspiration and wild protection of his disclosures kept on driving him, starting with one clash then onto the next with different researchers[1].

By most records, Newton’s residency at the public was overbearing and despotic; he had the option to control the lives and professions of more youthful researchers with supreme force^[1].

In 1705, in a discussion that had been preparing for quite a while, German mathematician Gottfried Leibniz openly blamed Newton for copying his examination, asserting he had found little analytics quite a while before the distribution of Principia. In 1712, the Royal Society named an advisory group to research the issue. Since Newton was the leader of the public, he had the option to select the panel’s individuals and supervise its examination. As anyone might expect, the panel closed Newton’s need over the disclosure^[1].

Sir Isaac Newton (My First Science Biography)

Last Years:

At the finish of this life, Newton inhabited Cranbury Park, close to Winchester, England, with his niece, Catherine (Barton) Conduitt, and her better half, John Conduitt^[1].

Newton had gotten one of the most well-known men in Europe. His logical revelations were unchallenged. He additionally had become rich, contributing his sizable pay shrewdly and presenting sizable endowments to noble cause.

Regardless of his notoriety, Newton’s life was a long way from great: He never wedded or made many companions, and in his later years, a mix of pride, weakness, and side outings on unconventional logical requests drove even a portion of his couple of companions to stress over his psychological steadiness^[1].

Death:

When he arrived at 80 years old, Newton was encountering absorption issues and needed to change his eating routine and versatility. In March 1727, Newton experienced serious agony in his midsection and passed out, never to recapture cognizance. He passed on the following day, on 31st March 1727, at 84 years old^[1].

Works of Newton:

Published in his lifetime^[2]:

De analysi per aequationes numero terminorum infinitas written in the year 1669 and was published in the year 1711)
Of Natures Obvious Laws & Processes in Vegetation, it was unpublished, c. 1671–75)
De Motu corporum in gyrum in the year 1684.
Philosophiæ Naturalis Principia Mathematica in the year 1687.
Scala graduum Caloris. Calorum Descriptiones & signa in the year 1701.
Opticks in the year 1704.
Reports as Master of the Mint between the year 1701–1725.
Arithmetica Universalis in the year 1707.

Published after his death^[2]:

“The System of the World” in the year 1728 Mundi systemate is known as
Optical Lectures in the year 1728
The Chronology of Ancient Kingdoms Amended in the year 1728
Observations on Daniel and The Apocalypse of St. John in the year 1733
Method of Fluxions written in the year 1671 and published in the year 1736
A Historical Account of Two Notable Corruptions of Scripture in the year 1754

References:

1. 30th November 2020; Available from: biography

2. 30th November 2020; Available from: wikipedia

3. 30th April 2021; Available from: physicsaboutIsaac Newton Biography, facts and Gravity Laws of Motion3. 30th April 2021; Available from: physicsabout